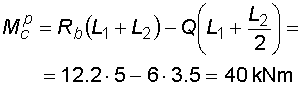F = 10 kN, q = 2 kN/m.
Opravena chyba - L2=3 m.
Řešení
1) Výpočet reakcí
Nejprve nahradíme spojité rovnoměrné zatížení q náhradním břemenem Q :
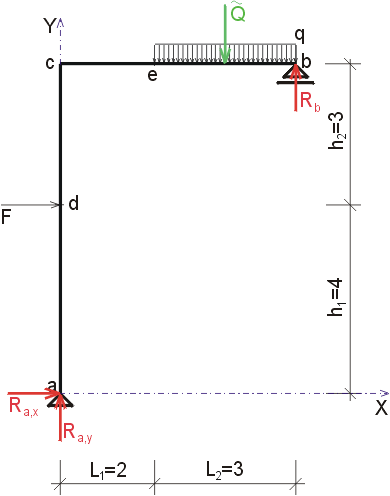
Nyní si naznačíme reakce. Bod a je podepřen pevným neposuvným kloubem, vzniknou v něm tedy dvě složky reakcí Ra,x a Ra,y. Bod b je podepřen posuvným kloubem, vznikne v něm tedy jedna složka reakce Rb. Složky reakcí určíme z podmínem rovnováhy :

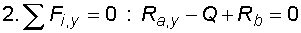


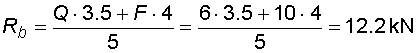
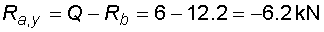
Vidíme, že princip výpočtu reakcí se neliší od předchozích příkladu.
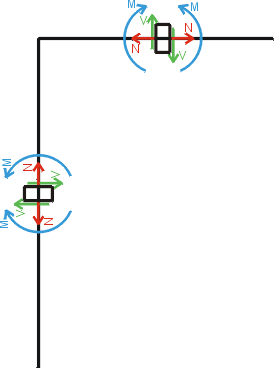
1) Výpočet vnitřních sil
Při výpočtu vnitřních sil si musíme uvědomit, že na lomeném nosníku vyvová zatížení na různých částech různé vnitřní síly. Zatížení působící v ose x vyvolává na svislé části posouvající síly, na vodorovné části normálové síly. Zatížení působící v ose y vyvolává na svislé části normálové síly, na vodorovné části posouvající síly. Tato skutečnost je i patrná z obrázku konvence kladných vnitřních sil na lomeném nosníku. Dále si pamatujme, že zatížení, které na jedné části nevyvolá ohybový moment, může jej vyvolat na jiné části (viz. příklad 9.2).Stejně jako u všech konstrukcí, i zde můžeme určovat vnitřní síly zprava nebo zleva tak, aby byl výpočet co možná nejjednodušší. V našem příkladě budeme určovat vnitřní síly na svislé části zleva, na vodorovné zprava.
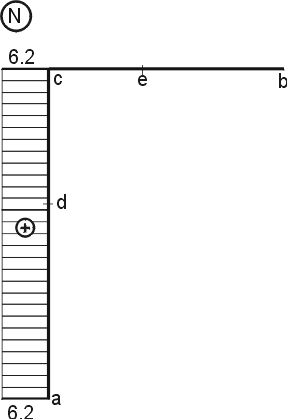
Normálové síly
Svislá část a-c : na této části působí v ose nosníku pouze reakce Ra,y. Proto po celé délce svislé části bude normálová síla konstantní.


Vodorovná část c-b : na této časti nepůsobí v ose nosníku žádné zatížení, proto normálová síla na této části je po celé délce nulová.
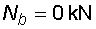
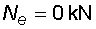
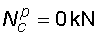

Posouvající síly
Svislá část a-c : na této části působí kolmo na osu nosníku reakce Ra,x a síla F. Posouvající síly budou tedy po částech konstantní a budou mít tyto velikosti :
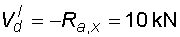


Vodorovná část c-b : na této časti působí kolmo na osu nosníku reakce Rb a spojité rovnoměrné zatížení q. Posouvající síly budou tedy mezi body c,e konstantního průběhu a mezi body e,b budou mít průběh lineární. Velikosti posouvajících sil budou následující :




Ohybové momenty
Svislá část a-c : na této části působí reakce Ra,x, Ra,y a síla F. Reakce Ra,y však prochází osou nosníku a nevyvolá tedy k žádnému bodu ohybový moment. Ten vyvodí pouze reakce Ra,x a síla F. Protože posouvající síla je mezi body a,d konstantní, bude průběh momentů mezi těmito body lineární. Mezi body d,c je posouvající síla nulová, průběh momentů bude tedy v tomto místě konstantní. Velikosti momentů v místech a,d,c je :
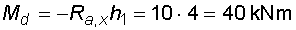
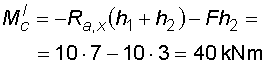
Vodorovná část c-b : na této časti působí kolmo reakce Rb a spojité rovnoměrné zatížení q. Obě tato zatížení vyvolají ohybový moment. Protože je posouvající síla mezi body c,e konstantní, bude průběh momentů v této části lineární. Mezi body e,b je průběh posouvajících sil lineární, tudíž průběh momentů bude mít tvar paraboly 2°. Velikosti momentů v jednotlivých místech je :